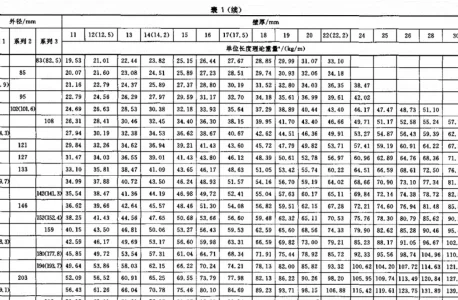
钢管的理论重量计算公式(行业算法)
在不锈钢行业中,为了提高效率,对于钢管的理论重量[1],普遍采用以下这种算法:
重量kg = (外径mm - 壁厚mm) × 壁厚mm × 行业常数0.02466 × 长度m
其中的行业常数0.02466,来自:
材料比重*π/1000,
并非像π那样真的恒久不变的常数,如:
235的比重为:7.85,常数=7.85*3.1416/1000≈0.02466
304的比重为:7.93,常数=7.93*3.1416/1000≈0.02491
321的比重为:8.03,常数=8.03*3.1416/1000≈0.02523
例如:
一根外径89mm,壁厚8mm,长6米的304钢管,其重量计算为:
(89-8) * 8 * 0.02491 * 6 ≈ 96.850 kg
常规的数学计算方法
如果从一个外行的角度来看的话,可能会被这个行业算法搞的一头雾水了(我当年就这样),为啥这么算呢?有啥依据呢?这个0.02466是个啥呢?
那么,就从容易理解的角度,用普通的数学方式来算一下,就是将钢管视为一个空心圆柱体,最直观的算法就是(这本比算环形面积*高复杂点,不过更直观):
外径大圆柱体重量 - 内部空心体重量
还是上例中的这根钢管,计算如下:
先把钢管当做实心圆柱体计算:
其直径89mm,半径44.5mm,长度6m,比重7.93
[(3.1416 * 44.5^2 * 6) * 7.93] / 1000 ≈ 296.002 kg
再计算中间空心部分:
其直径89-8*2=73mm,半径36.5mm,长度6m,比重7.93
[(3.1416 * 36.5^2 * 6) * 7.93] / 1000 ≈ 199.141 kg
最后圆柱-空心=空心圆柱也就是光管重量:
296.002 - 199.141 = 96.861 kg
两种算法结果一致
实际计算中对于行业常数和π的取值精度不同,两种方法会有细微的差别,比如这里的两种算法就产生了约0.11kg的差异,提高圆周率的精度和常数精度就可以减小这个差异。
不代入实际数字,只算公式的话,两种算法的结果是完全一致的。
两种算法结果一致 为啥总有人算错 ?
经过比较,可见两种计算方法的结果是一致的,很多时候不同的人算出来会有误差,最容易出错的地方就是有人会习惯性的忽略行业常数的值,日常主要卖碳钢的,用惯了7.85、用惯了0.02466,在计算不锈钢材料的时候,很容易就直接带入,而忽略了不锈钢的比重不同,常数也应该随之变化这个问题。
另一个有趣的错误
多年前,当我还是一个萌新的时候,工作相关有时候也想自己计算一下钢管重量,拿到了行业公式,也注意到了不同材料的常数应该不同。但是,算了几次都错误,行业算法和数学普通计算就是结果不一致,头大。出于好学精神,想要研究一下,从普通数学到这个行业公式的简化过程,以便发现自己到底哪里错误。
结果,终于找到自己的一个低级错误,还是以上面钢管为例,外径89mm的钢管,壁厚8mm,我当年在计算普通数学方法的时候,居然把中空体的直径直接就算作89-8(应该是73),忽略了直径和壁厚的关系,内直径 = 外直径 - 壁厚 * 2,当然会计算错误了。后来这些年中,又有不少人问过我这个问题,居然,他们中依然有人犯跟我当年一样的直径-壁厚错误。给予温馨提示的同时,心里觉得好安慰,原来我不是唯一的傻傻TT。
- 理论重量,行业内又叫做“检尺”,即根据材料的理论尺寸和比重计算其重量。与之相对的为:过磅重量,又称“检重”或“检斤”,即按照过磅称重的结果为依据计算重量。至于理论计重和过磅计重哪个更合理,或者哪个更划算,真的是见仁见智了。又需要的朋友可以参考一下《不锈钢理论和过磅价格换算》。 ↩︎